สำหรับใครที่สนใจเรื่องแนวพิศวงอยู่แล้ว น่าจะคุ้นเคยกับภาพของแถบโมเบียสหรือ Mobius strip อยู่บ้าง (สะกดได้หลายอย่าง เช่น Moebius, Möbius) แต่สำหรับใครที่เพิ่งเห็นภาพนี้ครั้งแรก ก็อาจสงสัยว่ามันคืออะไร เกี่ยวกับการเดินทางข้ามเวลาอย่างไร
.
วันนี้สารคดีเลยถือโอกาสมาแนะนำแถบโมเบียสให้เข้าใจกันง่ายๆ เพราะอาจมีบางคนเพิ่งเคยเห็นแว่บๆ เมื่อเร็วๆ นี้ หรือบางคนก็อาจจะได้เห็นในอนาคตเร็วๆ นี้
***เรื่องนี้ไม่มีสปอยล์***
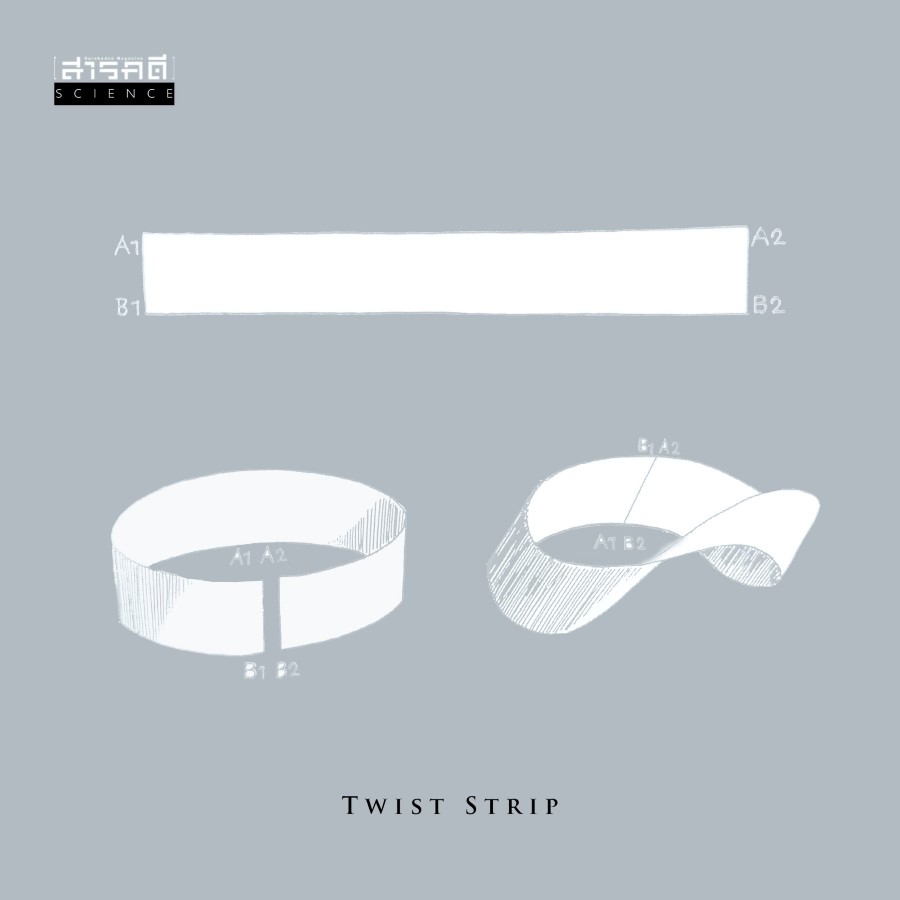
TwistStrip
โดยปรกติถ้าเราเอาแถบกระดาษ (หรือจะนึกถึงริบบิ้นก็ได้) ยาวๆ มาต่อหัวท้ายให้เป็นวง ก็จะได้วงแถบกระดาษปรกติตามรูปซ้าย แต่ถ้าก่อนจะต่อหัวท้าย เราบิดแถบริบบิ้นพลิกแล้วค่อยต่อกันเป็นวง ก็จะได้แถบโมเบียสตามรูปขวา
คนที่มีหัวคิดขี้เล่นทำแถบโมเบียสขึ้นครั้งแรก คือนักคณิตศาสตร์ชาวเยอรมัน นามว่า ออกัสตุส โมเบียส (Augustus Moebius) เขาเคยเป็นลูกศิษย์ของ เกาสส์ นักคณิตศาสตร์ผู้ยิ่งใหญ่ (Carl Friedrich Gauss)
โมเบียสคิดแถบโมเบียสเมื่อปี ค.ศ. 1848 เพราะฉะนั้น เรากำลังดูรูปทรงที่มีอายุถึง 171 ปีแล้ว
OnePlane, #One Edge
แม้จะมองดูผ่านๆ แล้วเหมือนว่ามีด้านในกับด้านนอก และมีสองขอบ เช่นเดียวกับวงแถบปรกติ แต่เรื่องพิศวงของแถบโมเบียส คือมันมี “ด้านเดียว” และ “ขอบเดียว”
หน้าเดียว คือถ้าเราเริ่มทาสีบนผิวกระดาษด้านไหนก็ได้
จะเป็นด้านที่เราคิดว่าเป็นด้านใน หรือด้านที่เราคิดว่าเป็นด้านนอกก็ได้ ทาสีไล่ไปทางเดียวกันเรื่อยๆ เชื่อไหมว่า ในที่สุดเราก็จะทาสีจนเต็มทุกด้าน ถ้าเริ่มจากด้านนอก มันก็จะพาเราไปถึงด้านใน แล้ววนออกมาด้านนอก
หรือจะเอาดินสอมาลากเส้นไปเรื่อยๆ เส้นนั้นก็จะมาเจอจุดเริ่มต้นได้เอง ไม่ต้องลากเส้นใหม่
หรือถ้าจินตนาการว่า เราเป็นมดตัวเล็กๆ เราสามารถเดินบนพื้นแถบริบบิ้นโมเบียสไปเรื่อยๆ เราก็จะเดินวนกลับมาเจอ ณ จุดตั้งต้น โดยไม่ต้องเดินไต่ข้ามขอบกระดาษ
และสำหรับระยะการเดินนั้นจะเป็น 2 เท่าของความยาวแถบตั้งต้น
ขณะที่การต่อวงแถบกระดาษแบบปรกติ ด้านในกับด้านนอกจะแยกฝั่งกันชัดเจน
ส่วนขอบเดียว คือถ้าเราลองใช้นิ้วแตะขอบกระดาษตรงไหนก็ได้ของแถบโมเบียส ไล่ไปเรื่อยๆ ในที่สุดเราจะกลับมาถึงจุดเริ่มต้นที่แตะขอบเช่นกัน
อ่านแล้วอย่าเพิ่งเชื่อ ลองพิสูจน์ดูเองเลย
MoebiusStripII
เป็นภาพวาดที่มีชื่อเสียงมากอีกภาพหนึ่งของศิลปินจินตนาการมากล้น เมาริตช์ เอสเชอร์ (Maurits Escher 1898-1972)
เอสเชอร์คลั่งไคล้เรื่องของมิติวนลูป และการบิดผันของรูปทรง ทั้งบนระนาบสองมิติและรูปทรงสามมิติและสร้างภาพลวงตาของสิ่งของหลายอย่างที่ไม่อาจเกิดขึ้นจริงขึ้น
เป็นงานศิลปะอันน่างงงวยสำหรับทุกคนมาจนถึงปัจจุบัน
เช่น ภาพสายน้ำที่ไหลจากหอคอยอาคารลงมาชั้นล่าง แต่ในที่สุดก็ไหลวนจากชั้นล่างขึ้นไปข้างบนหอคอยได้
ภาพมดไต่แถบโมเบียสของเอสเชอร์ภาพนี้ ถือเป็นหนึ่งในไม่กี่ภาพที่เหมือนภาพลวงตา แต่กลับเป็นสภาวะที่อาจเกิดขึ้นได้จริง
เขาวาดภาพนี้ในปี 1963 นอกจากนี้เขายังวาดภาพ Moebius I ไว้ด้วยในปี 1961
KleinBottle
คิดค้นขึ้นโดย Felix Klein นักคณิตศาสตร์ชาวเยอรมันเช่นกัน (1849-1925) ขวดนี้เปรียบเสมือนแถบโมเบียสในรูปทรงมีปริมาตร คือเป็นขวดที่มีพื้นผิวด้านเดียว พื้นผิวด้านในขวดก็คือพื้นผิวที่ต่อเนื่องกับผิวด้านนอกขวด พื้นผิวด้านนอกขวดก็ต่อเนื่องถึงผิวด้านในขวด
ถ้าไม่เชื่ออีกละก็ ต้องลองไล่ไปตามผิวขวดดู
และถ้าผ่าขวดแบบครอสส์เซกชั่น เราจะได้แถบโมเบียสสองอัน
เรื่องน่าพิศวงอื่นๆ
- ผู้คนสมัยโรมันโบราณก็อาจรู้จักแถบโมเบียสแล้ว โดยปรากฏอยู่ในภาพกระเบื้องโมเสกคู่กับเทพเจ้าแห่งนิรันดร Aion ที่เวลาหมุนวนเป็นวัฎจักร (ภาพดูคล้ายโมเบียส แต่ก็อาจไม่ใช่ เพราะ Aion ในภาพอื่นๆ จะอยู่กับวงแหวนธรรมดา)
- ถ้าเอากรรไกรตัดวงแถบปรกติตามเส้นที่ลากไว้แบ่งครึ่งตรงกลางแถบ เราจะได้วงแถบสองวง แยกกันแน่นอน แต่ถ้าตัดวงแถบโมเบียส สุดท้ายเราจะได้วงแถบเดียวที่หมุนบิดต่อกันอยู่
- ถ้าเอากรรไกรตัดวงแถบโมเบียสตามเส้นที่ลากไว้ที่ระยะ 1 ใน 3 ของความกว้างแถบ สุดท้ายเราจะได้วงแถบโมเบียสสองวง เป็นวงใหญ่หนึ่งวง และมีวงเล็กคล้องอยู่ข้างใน
- นักเคมีสังเคราะห์โมเลกุลที่ต่อกันเป็นรูปร่างตามแถบโมเบียส มีชื่อสารว่า tetra hydroxymethylethylene หรือชื่อย่อว่า Tris (THYME)
ส่วนแถบโมเบียสจะเกี่ยวกับการเดินทางข้ามเวลาอย่างไร ขอปล่อยให้เป็นจินตนการของผู้อ่านนะขอรับ
สำหรับผู้เขียน คิดว่าการเดินทางผ่านรูหนอนอวกาศกับรูปทรงขวด Klein Bottle ดูมีอะไรจะคล้ายๆ กันอยู่บ้าง